Diffusion Tree Sampling: Scalable
inference-time alignment of diffusion models

Vineet Jain,    Kusha Sareen,    Mohammad Pedramfar,    Siamak Ravanbakhsh
School of Computer Science, McGill University
Mila - Quebec Artificial Intelligence Institute
Paper Code (coming soon) arXiv

Diffusion Tree Sampling is an anytime algorithm that performs a global search in the space of denoising trajectories, turning additional compute budget into steadily better samples.
Shown above: prompt "cat" with aesthetic reward.

Abstract

Adapting a pretrained diffusion model to new objectives at inference time remains an open problem in generative modeling. Existing steering methods suffer from inaccurate value estimation, especially at high noise levels, which biases guidance. Moreover, information from past runs is not reused to improve sample quality, resulting in inefficient use of compute. Inspired by the success of Monte Carlo Tree Search, we address these limitations by casting inference-time alignment as a search problem that reuses past computations. We introduce a tree-based approach that samples from the reward-aligned target density by propagating terminal rewards back through the diffusion chain and iteratively refining value estimates with each additional generation. Our proposed method, Diffusion Tree Sampling (DTS), produces asymptotically exact samples from the target distribution in the limit of infinite rollouts, and its greedy variant, Diffusion Tree Search (DTS$^\star$) performs a global search for high reward samples. On MNIST and CIFAR-10 class-conditional generation, DTS matches the FID of the best-performing baseline with up to $10\times$ less compute. In text-to-image generation and language completion tasks, DTS$^\star$ effectively searches for high reward samples that match best-of-N with up to $5\times$ less compute. By reusing information from previous generations, we get an anytime algorithm that turns additional compute budget into steadily better samples, providing a scalable approach for inference-time alignment of diffusion models.

Reward vs NFEs
Image samples for different methods
Reward vs NFEs
Text samples for different methods

Scaling inference budget

Scaling inference budget - 1,000 NFEs
1,000 NFEs → Inference budget → 100,000 NFEs

Approach Overview

Comparison of Best-of-N, SMC, and DTS

Left: Best-of-N denoises multiple samples using the base diffusion model and selects the one with the highest reward.
Center: SMC maintains a population of particles and resamples based on an estimate of the value function.
Right: DTS and DTS* maintain a tree that accumulates information across multiple rollouts and backs up the terminal reward to refine value estimates. The diagram illustrates the four phases: selection, expansion, rollout, and backup.

Our method starts from two concrete desiderata for inference-time steering:

  • (D1) exploit low-noise timesteps—where rewards are trustworthy—to revise earlier, high-noise decisions;
  • (D2) turn extra compute into better samples rather than merely more particles, yielding an anytime algorithm.

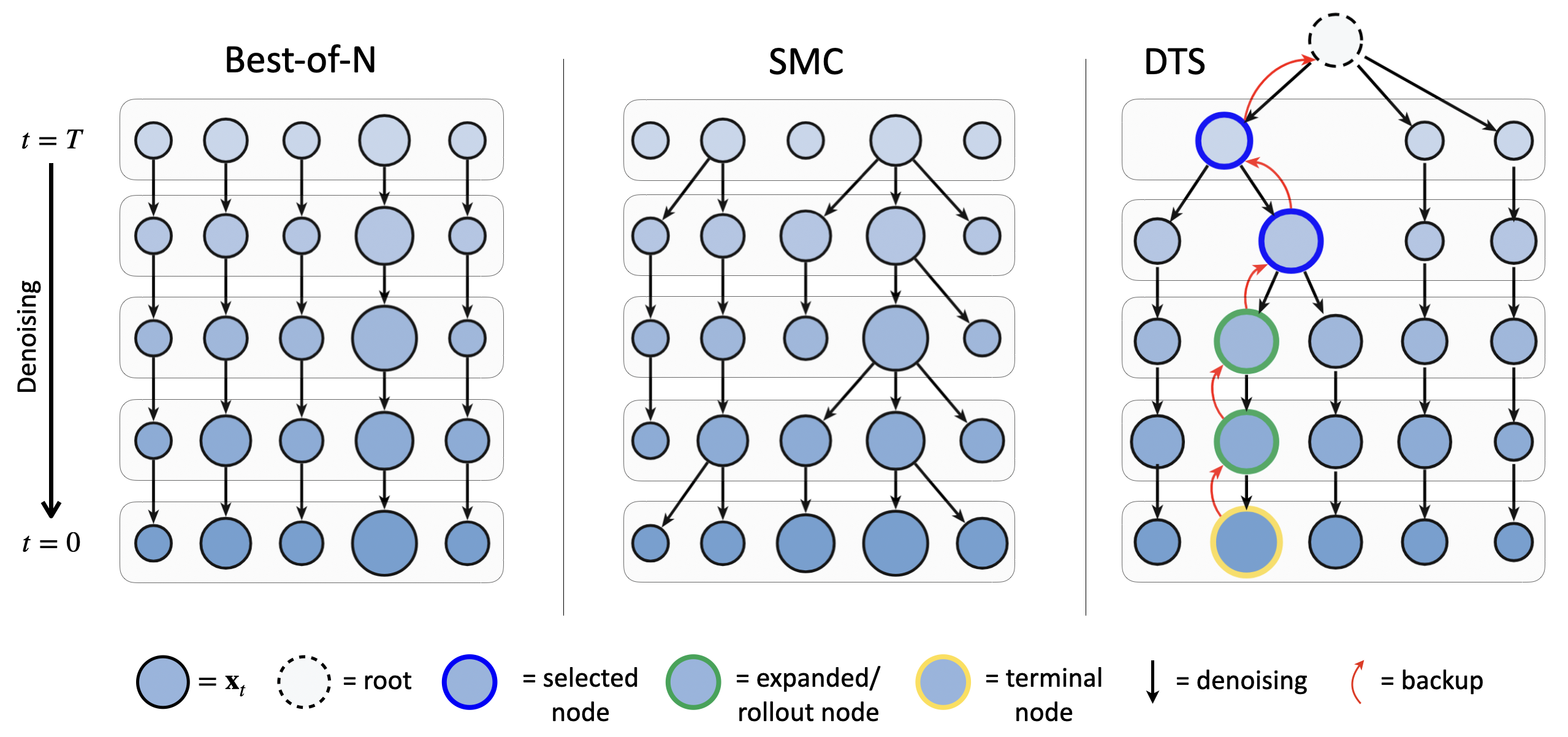
Reverse diffusion as a search tree

Because the learned reverse chain $p_\theta(x_{t-1} | x_t)$ is Markov with finite horizon $T$, we reinterpret the denoising process as a depth-$T$ tree in $\mathbb{R}^d$. A node at depth $t$ stores the noisy latent $x_t$, a running soft-value estimate $\hat{v}(x_t)$, and a visit count; each edge is a stochastic denoising step. This framing allows us to keep track of information across multiple denoising trajectories, including estimates of the soft value function, which helps with global credit assignment.

Diffusion Tree Sampling & Search

Tree traversal alternates selection → expansion → rollout → backup:

  1. Selection: Starting from the root, sample children according to a Boltzmann policy $\propto \exp(\lambda \hat{v}(\cdot))$.
  2. Expansion: If the selected node has fewer children than the maximum and $t > 0$, draw a new child from $x_{t-1} \sim p_\theta(\cdot | x_t)$.
  3. Rollout: From the newly created node, perform a rollout till $x_0$ using $p_\theta$; every intermediate state is appended to the tree.
  4. Backup: Evaluate terminal reward $r(x_0)$ and update value estimates along the path using the soft Bellman backup.

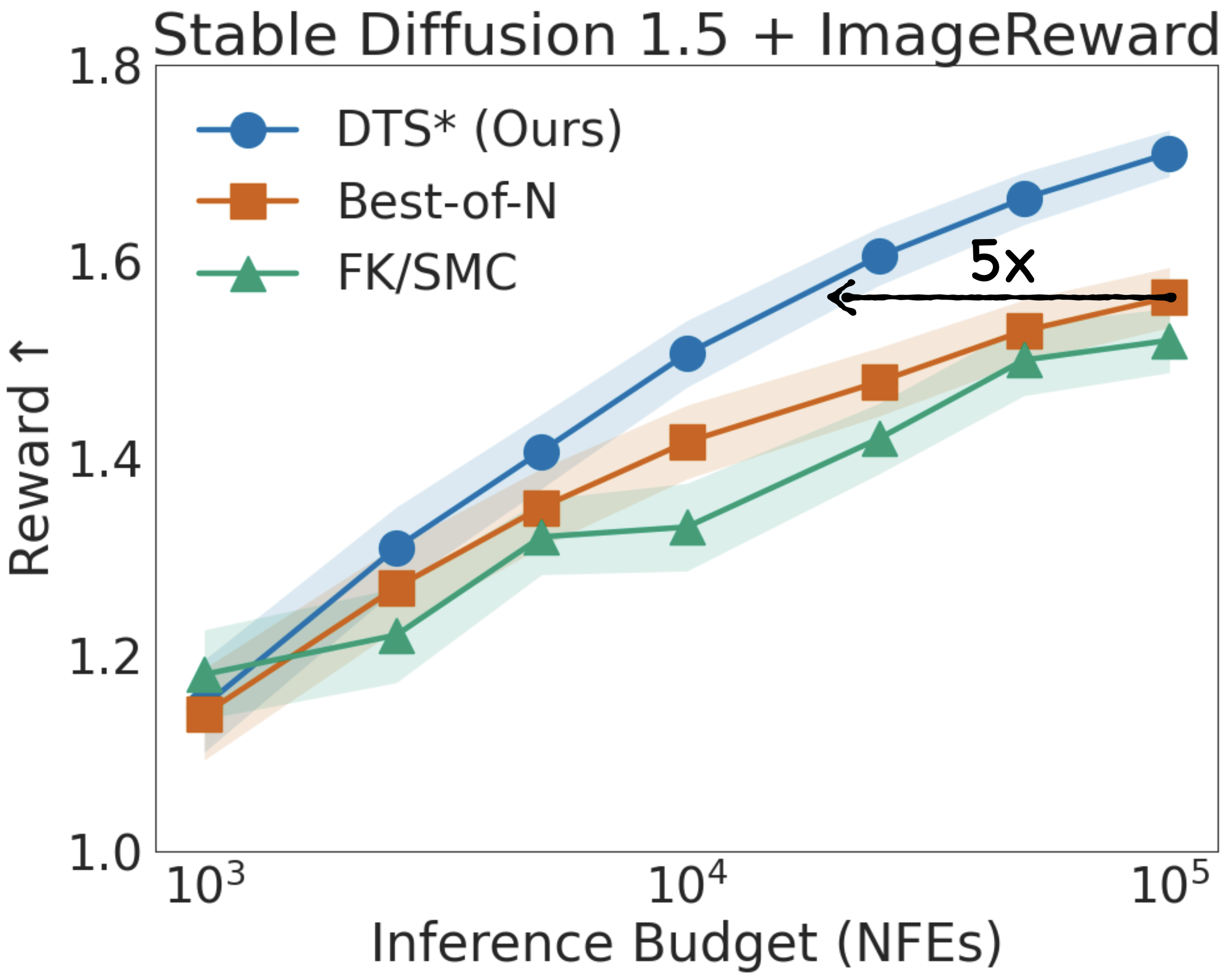
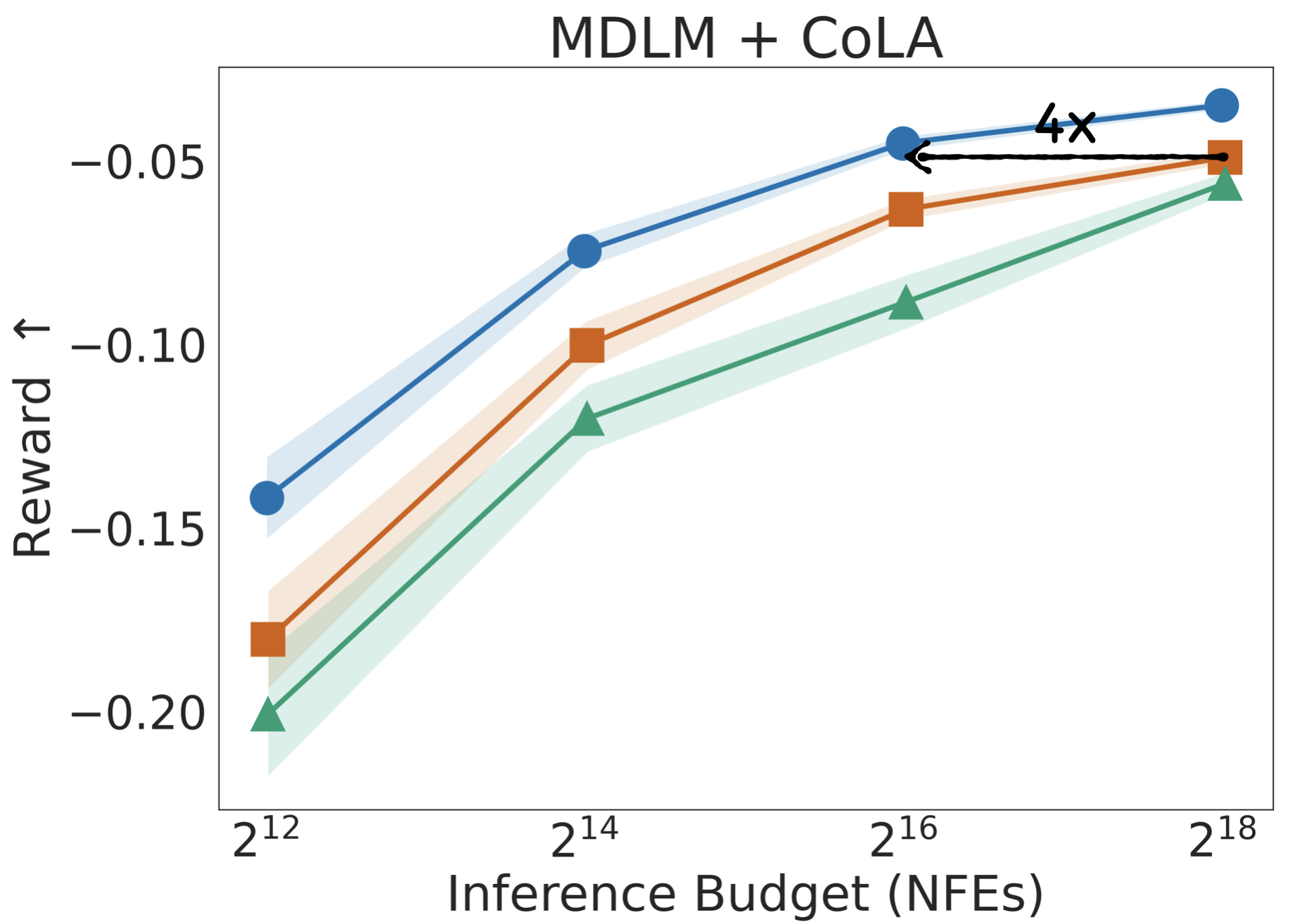
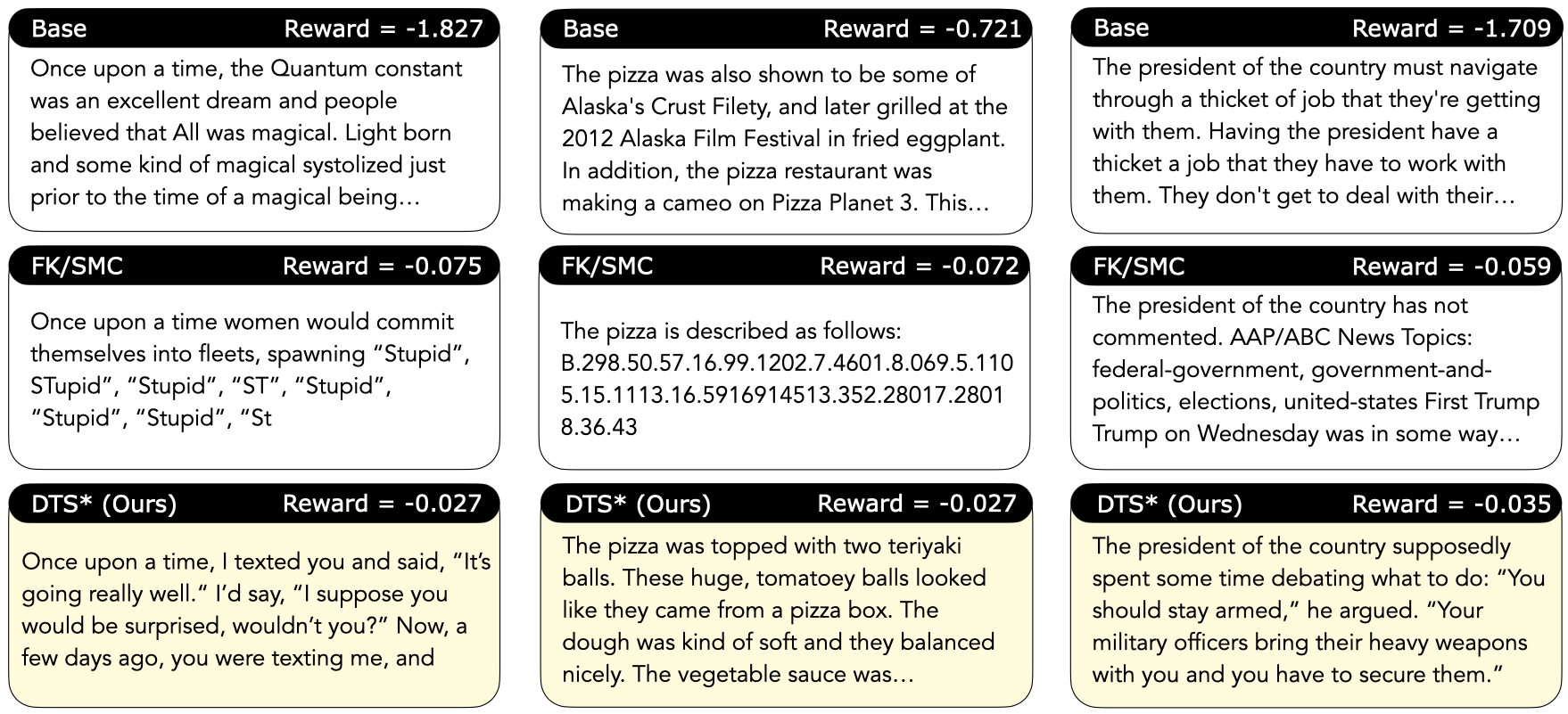
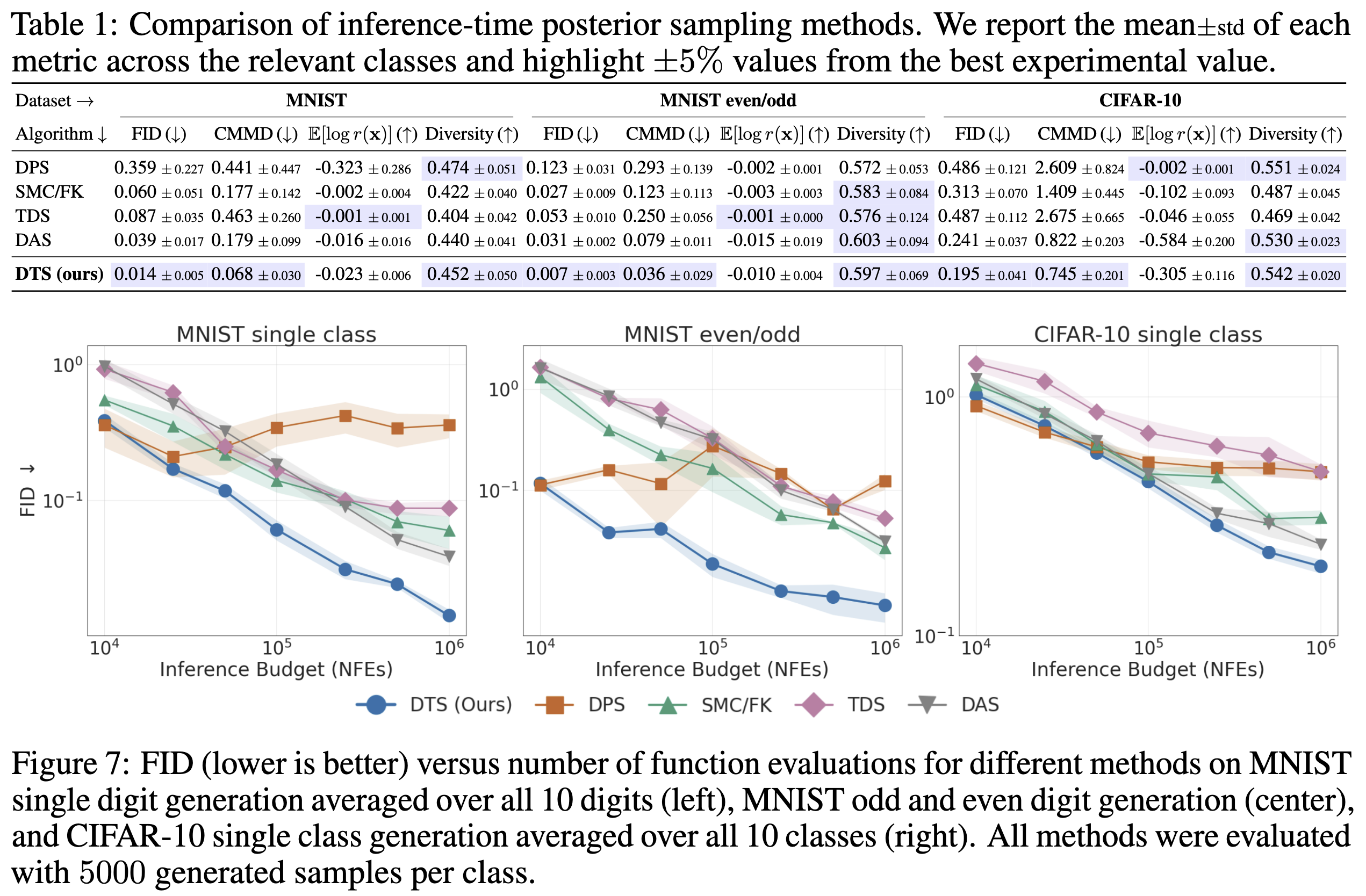
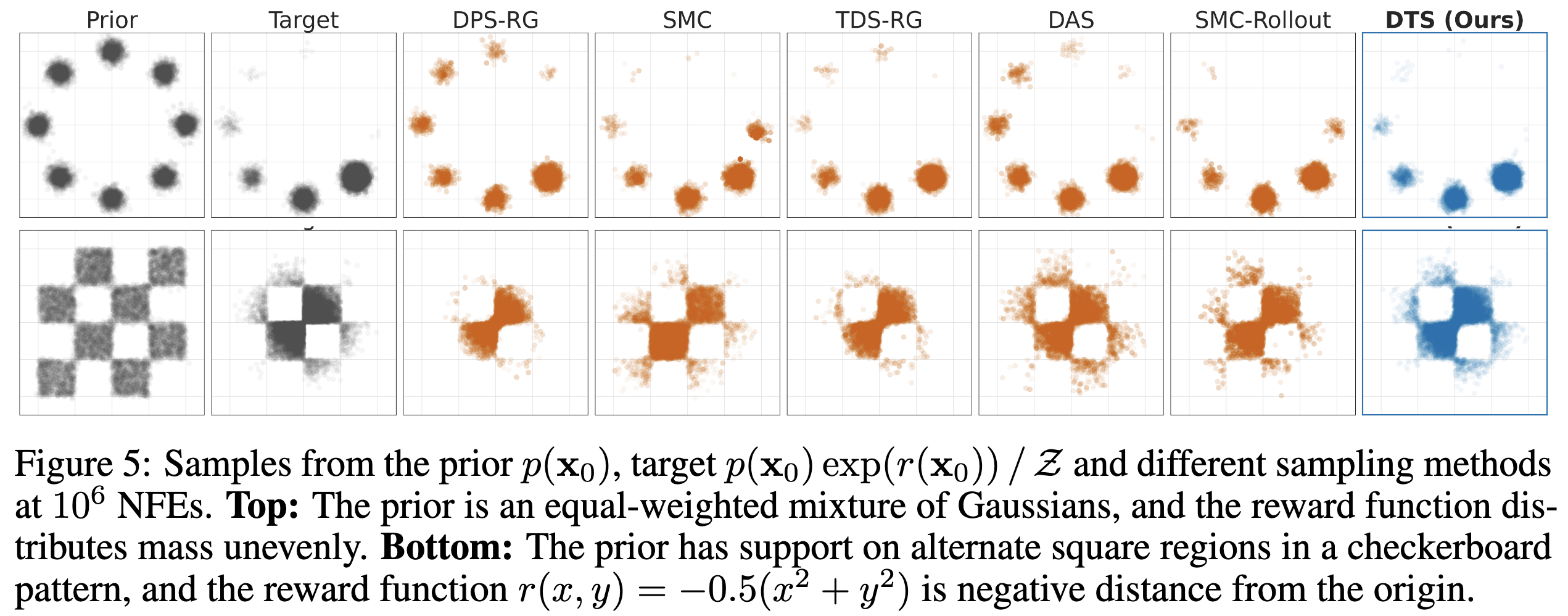
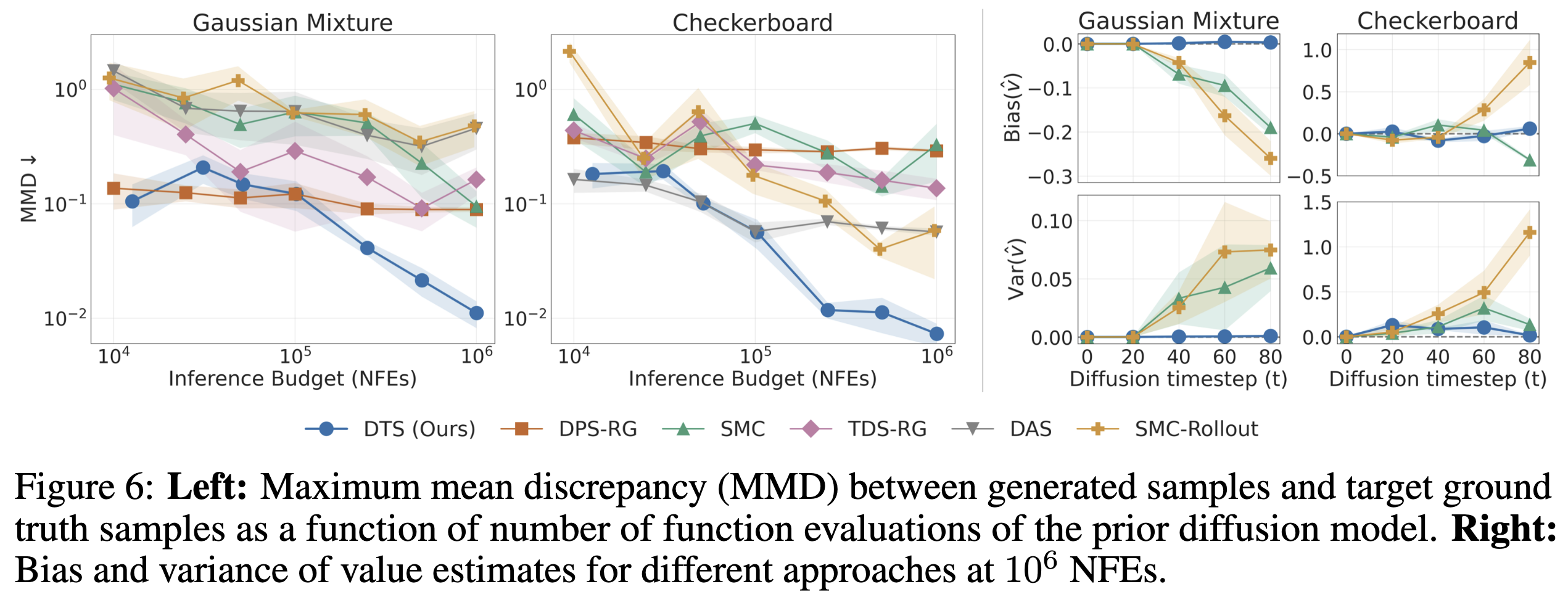
Repeating this loop yields Diffusion Tree Sampling (DTS), an anytime sampler whose empirical distribution provably converges to the target density $p_\theta(x) \exp(r(x))$. Switching the selection rule to greedy maximization produces Diffusion Tree Search (DTS$^\star$) to find high reward samples without over-optimization — no other code changes required.

Class-Conditional Generation ▼
FID vs Compute for MNIST and CIFAR-10
MNIST/CIFAR-10 sample comparisons
2D Dataset Experiments ▼
2D dataset experimental results
2D dataset experimental results

BibTeX

@article{jain2025diffusiontreesampling,
      title={Diffusion Tree Sampling: Scalable inference-time alignment of diffusion models}, 
      author={Vineet Jain and Kusha Sareen and Mohammad Pedramfar and Siamak Ravanbakhsh},
      journal={arXiv preprint arXiv:2506.20701},
      year={2025}
}